Extending Concrete Service Life in Marine Environments: A Long-Term Field Study and Lifecycle Prediction

Introduction

Accurate service life prediction is fundamental to the design and maintenance of reinforced concrete structures exposed to aggressive environments. This study applies Fick’s Second Law of Diffusion to assess chloride ingress in Xypex-treated concrete panels, built in 1995, weighing over 20 tonnes and with a compressive strength of 40 MPa, installed in the splash zone and exposed to bulk chemicals, and fertilizers from off-loading operations at the Lascelles Wharf, Port of Geelong, Australia, estimating the time required for chloride concentrations to reach reinforcement depth and initiate corrosion.

Experimental Procedure (according to fib Bulletin 34)

• Chloride Profiling: Chloride concentration at multiple depths was measured using core samples with known exposure durations (19 years-old and 26 years-old).
• Diffusion Coefficient Calculation: The diffusion coefficient was derived from chloride concentration gradients.
  • $D_{e f f(t)}=D_{e f f\left(t_0\right)} *\left(\frac{t}{t_0}\right)^{-m}$
  • $D_{e f f\left(t_0\right)}$ :initial diffusion coefficient (derived from chloride concentration test data).
  • $t_0$ : reference time.
  • $m$ : was empirically determined by analyzing the time-dependent reduction of the effective chloride diffusion coefficient $\left(D_{e f f}\right)$.
    • $m=\frac{\Delta \log t}{\Delta \log D_{e f f}}$ .
• Predictive Modeling: Based on experimental diffusion coefficients and cover depth data, the service life was estimated using Fick’s Second Law of Diffusion
  • $C(x, t)=C_S\left(1-\operatorname{erf}\left(\frac{x}{2 \sqrt{D_{e f f}(t)} \cdot t}\right)\right)$
    • $C(x,t)$: chloride concentration at depth x and time t.
    • $C_S$: surface chloride concentration.
    • erf: error function.
    • $D_{e f f\left(t_0\right)}$ : effective chloride diffusion coefficient at time t.
    • $x$: depth in concrete.

Results and Discussion:

• Predicted Service Life in 2014 at Characteristic Cover Depth (51 mm): 164 years.
• Predicted Service Life in 2021 at Characteristic Cover Depth (51 mm): 187 years.

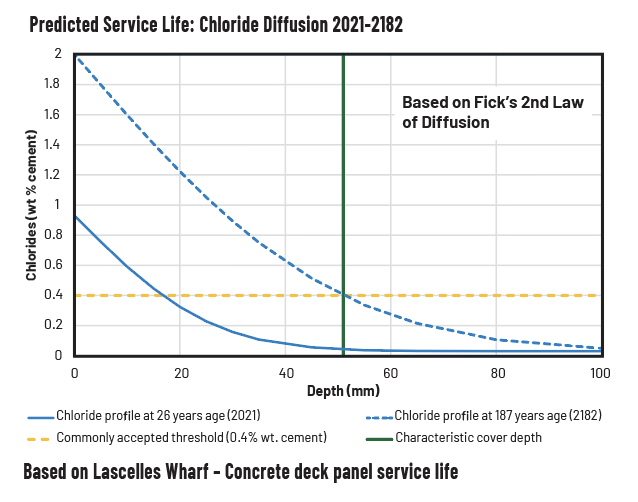
These results confirm that Xypex-treated concrete decreases the chloride diffusion coefficient over time, supporting its long-term durability and extended service life.

Conclusion

The 2014 vs. 2021 service life analysis validates the ability of Xypex-treated concrete to improve its chloride resistance properties over time. The decrease of the diffusion coefficient over time reinforces the efficacy of the Xypex Crystalline Technology in extending service life and mitigating corrosion risk.